هندسة المثلثات: ما هو مجموع زوايا المثلث

كم مجموع زوايا المثلث

مجموع زوايا المثلث داخل هذا الشكل يساوي 180 درجة. يمكن استخدام مجموع الزوايا الداخلية للمثلث لحساب مجموع الزوايا الداخلية لجميع المضلعات. في الواقع، فان القانون الخاص بمجموع الزوايا الداخلية مشتقة من العلاقة الهندسية بين المثلث والمضلعات الأخرى. في هذا المقالة المقدمة لكم في موقع الرياضيات العربية التخصصي، سوف نعلمك كيفية حساب مجموع الزوايا الداخلية للمثلث وكيفية استخدامه لحساب مجموع الزوايا الداخلية للمضلعات الأخرى مع حل أمثلة مختلفة، تماماً كما فعلنا في مقالة أنواع المثلثات حسب الزوايا.

ما هو المثلث؟

سبق أن تعرفنا في مقال (ما هو المثلث؟) على تعريف المثلث، وهو أحد المضلعات ومن الاشكال الهندسية الأساسية التي تتكون من ثلاثة أضلاع.

من بين الاجزاء الرئيسية والمهمة للمثلث، يمكننا أن نشير إلى القاعدة (ضلع)، الارتفاع، الرأس (نقطة اتصال الاضلاع)، الزاوية الداخلية والزاوية الخارجية.

ما هي الزوايا الداخلية للمثلث؟

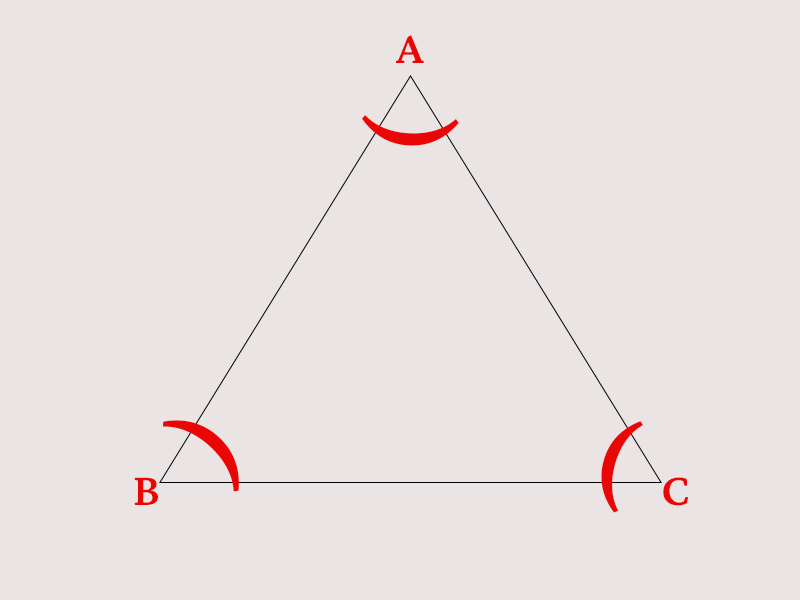
تسمى الزوايا الموجودة داخل اضلاع المثلث بالزوايا الداخلية للمثلث. المثلث له ثلاث زوايا داخلية. بينما تسمى الزوايا المكملة للزوايا الداخلية للمثلث بالزوايا الخارجية للمثلث.

كيفية مجموع زوايا المثلث

قد تعتقد أنه يتم الحصول على مجموع الزوايا الداخلية لأي مثلث عن طريق قياس كل زاوية بالطرق المباشرة (مثل المنقلة).

يجب أن نقول إنه ليست هناك حاجة للقيام بذلك لتحديد مجموع الزوايا الداخلية للمثلث، لأن هذا المجموع متساوي لجميع المثلثات.

مجموع الزوايا الداخلية للمثلث يساوي دائمًا 180 درجة. بعبارة أخرى:

180°= زاوية (c) + زاوية (b) + زاوية (a)

ما هو قانون مجموع الزوايا الداخلية للمثلث؟

بشكل عام، يتم حساب مجموع الزوايا الداخلية لجميع المضلعات باستخدام القانون التالي:

S=(n−2)×180°

• S: مجموع الزوايا الداخلية للمضلع
• n: عدد الاضلاع

أمثلة على حساب مجموع زوايا المثلث

جد مجموع الزوايا الداخلية للمثلث باستخدام القانون.

لحل هذا المثال، يجب ان نكتب قانون مجموع الزوايا الداخلية للمضلعات للمثلث:

S=(n−2)×180°

نعوض عدد الأضلاع في القانون ثم نحل المسألة:

S=(3−2)×180°

S=(1)×180°

S=180°

الخلاصة

بالنظر إلى أن مجموع زوايا المثلث يساوي دائمًا 180 درجة، يمكننا أن نستنتج أن أي مثلث مهما كان حجمه وشكله، فإن مجموع زواياه يكون دائمًا ثابتًا ويساوي 180 درجة. هذه الميزة الأساسية لعلم المثلثات مفيدة جدًا في حل المسائل الهندسية وتساعدنا على استخدام علم المثلثات في التحليل والتنبؤ بالسمات المختلفة للأشكال الهندسية، من الضروري ايضاً فهم أنواع الزوايا في الرياضيات لفهم افضل لهذا الموضوع.