كيف أحسب مساحة المثلث
مساحة المثلث من الدروس التي نتعلمها في بداية حياتنا الدراسية، ولكنها تبقى معنا حتى آخر سنة دراسية، وقد يكون لها استخدامات في الحياة اليومية. عندما نتحدث عن مساحة سطح المثلث، فإننا نبحث في الواقع عن المساحة المغلقة بين ثلاثة خطوط مستقيمة متصلة ببعضها البعض بشكل دقيق، مما يشكل شكلًا جذابًا يسمى المثلث.
ولكن كيف يمكننا الإجابة على أسئلة مثل كيف نحسب و ما هي مساحة المثلث؟ هذه المقالة المقدمة لكم على موقع الرياضيات العربية المتخصص من المفترض أن يساعدكم على تعلم كل ما تحتاجون إليه بشكل كامل، لذا ابقوا معنا.
لماذا تعلمه يعد امراً مهماً؟
الحساب الدقيق لمساحة المثلث له أهمية خاصة ويتم استخدامه في مجالات مختلفة من التخطيط الحضري والعمارة إلى الهندسة والسياحة الطبيعية.
ما هو مساحة المثلث؟
كما نعلم، المثلث هو شكل مغلق له ثلاثة أضلاع وثلاثة رؤوس. وبالتالي، مساحة المثلث هي إجمالي المساحة التي تشغلها الأضلاع الثلاثة للمثلث. بشكل عام، قانون مساحة المثلث هو 2 ÷ (الارتفاع × القاعدة).
ما هو تعريف القاعدة والارتفاع في المثلث؟
لفهم أفضل، تخيل أنك ترسم مثلثًا على الورق. إذا اخترت ضلعًا كقاعدة، ورسمت خطًا مستقيمًا من الرأس المقابل لذلك الضلع إلى الضلع المحدد بحيث يشكل مع ذلك الضلع زاوية قائمة (90 درجة)؛ يسمى الخط المرسوم ارتفاع المثلث.
القانون العام لحساب مساحة المثلث
يمكن حساب مساحة المثلث باستخدام قوانين مختلفة. على سبيل المثال، يستخدم قانون القاعدة والارتفاع لحساب المساحة عندما نعرف طول كل من الأضلاع الثلاثة. عندما نعرف طول ضلين و الزاوية المشكلة بينهما، يمكننا أيضًا استخدام الدوال المثلثية للعثور على المساحة.
ولكن مع كل هذا، عندما نحتاج إلى طريقة حساب مساحة المثلث، هناك قانون أساسي يمكن استخدامه، وهو على النحو التالي:
بالرموز
حيثُ تمثّل:
- A = Area: وهي تعني المساحة
- h=height: الارتفاع
- b=base: القاعدة
بالعربي
يمكنك كتابة القانون بالحروف العربية ايضاً:
2 ÷ (الارتفاع × القاعدة) =مساحة المثلث
ولكن في بعض الأحيان، يمكن للمدرس استخدام الحروف اللاتينية في الامتحانات مثل القوانين التي كتبناها لك أعلاه. إذا حفظتها، فلن تواجه أي مشاكل.
فهم أفضل لقانون مساحة المثلث
وفقًا للشكل أدناه، يمكنك فهم هذا القانون بدقة أكبر.
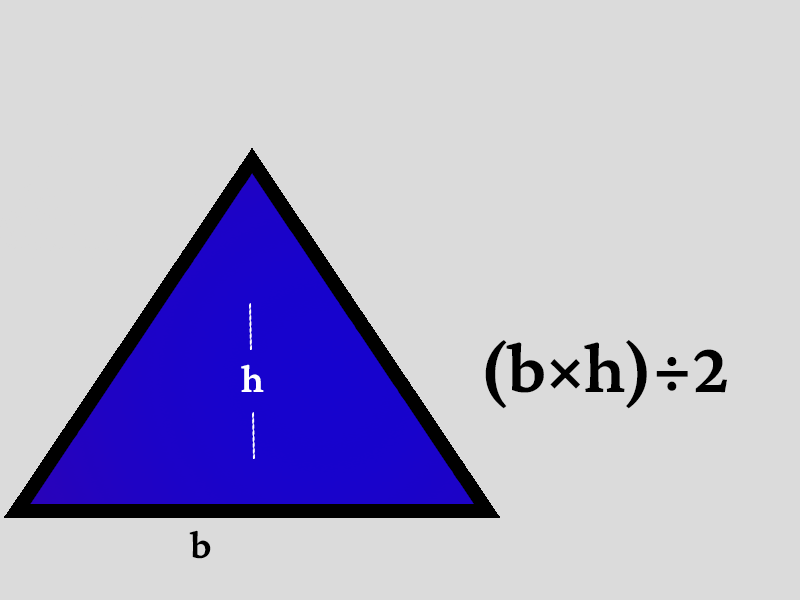
يمكن استخدام القانون العام لحساب مساحة المثلث قائم الزاوية والمثلثات الأخرى أيضًا.
أمثلة على حساب مساحة المثلث
السؤال الاول :
إذا كان لدينا مثلث ارتفاعه 5 وقاعدته 4، فكم تساوي مساحته بالسنتيمترات، استناداً لقانون مساحة المثلث؟
الجواب
وفقًا للقانون، يجب ان نعوض الأرقام ادناه للحصول على النتيجة المرجوة.
2 ÷ (5 × 4) = مساحة المثلث
من خلال حل المعادلة أعلاه، نحصل على الرقم 10، وهو مساحة هذا الشكل المعني.
إيجاد مساحة المثلث بصيغة هرون او هيرو (Heron’s formula)
ف تُستخدم صيغة هيرون عندما يكون لدينا ثلاثة أضلاع لمثلث ونحتاج إلى إيجاد مساحته باستخدام القانون التالي.
إن s هو نصف محيط المثلث (نصف مجموع طول أضلاع a،b،c) للفهم بشكل أفضل، يرجى الانتباه إلى الصيغة التالية.
أمثلة على صيغة هرون او هيرو
مثال: لديك مثلث بطول أضلاع a=7 و b=8 و c=9 كيف تجد مساحة هذه الشكل؟ الجواب: يجب اولاً حساب نصف محيط المثلث s :
بعد الحصول على قيمة s، يجب ان نعوضه في صيغة هرون كما يلي:
قانون مساحة المثلث بدلالة جيب إحدى زواياه
يمكن حساب مساحة المثلث باستخدام ضلعين و الزاوية بين هذين الضلعين، و هذه الطريقة تُعرف عادةً باسم “ضلع – ضلع – زاوية” أو “SAS“.
مساحة المثلث = ½ × الضلع الأول × الضلع الثاني × جيب الزاوية
يمكن كتابتها على النحو التالي:
أمثلة على مساحة المثلث بدلالة جيب إحدى زواياه
مع الأخذ في الاعتبار أن في الضلع الأول لمثلث = 4 و الضلع الثاني =6 و الزاوية بين هذين الضلعين =30° كيف سيتم حساب مساحة هذه الشكل؟
ملحوظة: قيمة جيب الزاوية 30 درجة تساوي ½
جدول قانون حساب مساحة المثلث
الجدول التالي يتضمن قانون طريقة حساب مساحة أنواع مختلفة من المثلثات التي تعتبر من أكثر الطرق شيوعًا في حساب مساحة هذه الشكل الهندسي، يمكنك استخدام الجدول التالي للإجابة على 90٪ من الأسئلة المتعلقة بالمساحة.
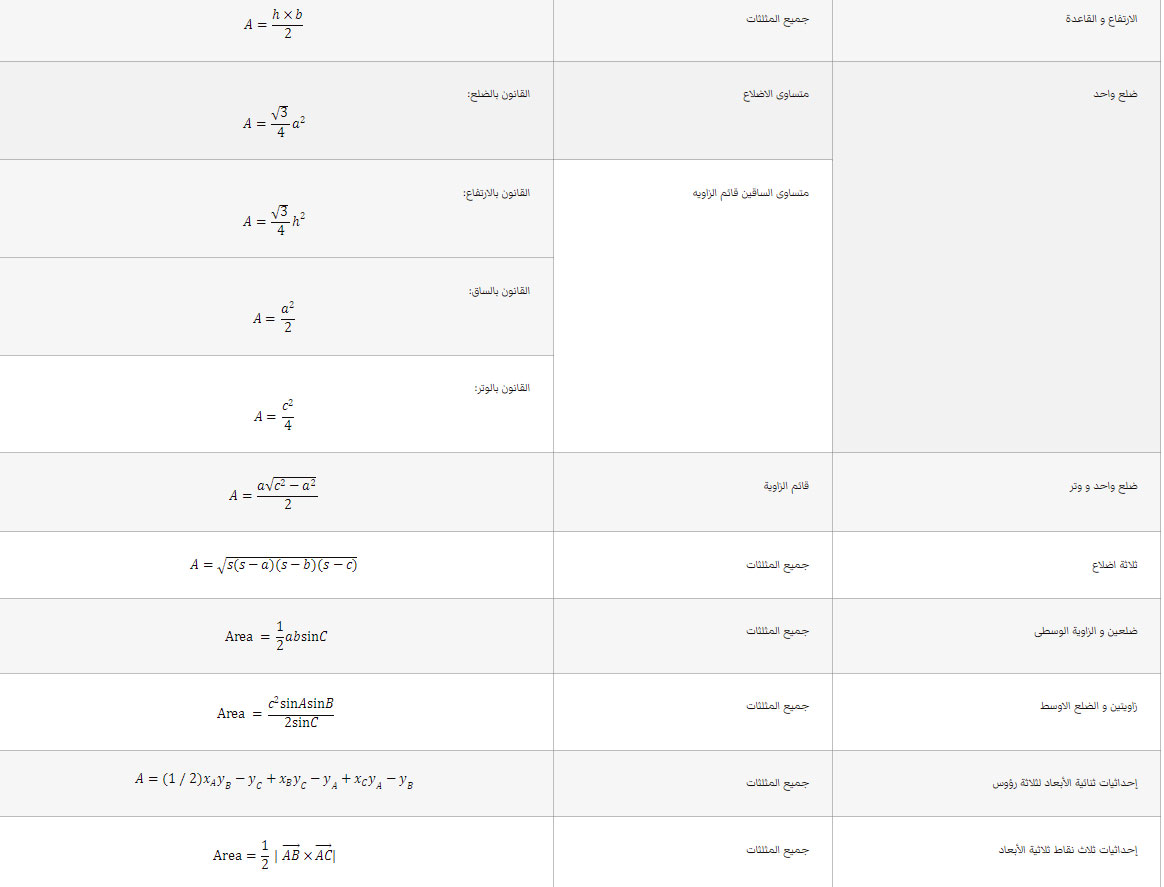
قوانين مساحة المثلث pdf
لقد اعددنا لكم هنا جدول المساحة في قالب pdf جميل
ايجاد المساحة في باقي المثلثات
في هذا القسم، سنتحدث عن مساحة المثلث القائم الزاوية ومتساوي الأضلاع معًا:
مساحة المثلث متساوي الاضلاع
المثلث متساوي الأضلاع هو مثلث ذات أضلاع متساوية كما هو واضح من اسمه. ان الأضلاع المتساوية في هذا الشكل تتيح حساب مساحة هذا المثلث باستخدام قانون خاص.
تُعرف العلاقة التي تم تقديمها في القسم السابق بالعلاقة العامة بين قاعدة المثلث وارتفاعه ومساحته. قانون مساحة المثلث متساوي الاضلاع مع الضلع a تساوي:
A=√3/4 × a 2
إذا كان ارتفاع هذا المثلث معروفًا، يمكن إعادة كتابة القانون أعلاه على النحو التالي:
A=√3/3 × h 2
قانون مساحة مثلث قائم الزاویه مع الوتر
المثلث القائم الزاوية هو مثلث رأسه 90 درجة، وأرجله قائمة الزاوية وقاعدته وارتفاعه متساويتان.
وفقًا لنظرية فيثاغورس، فان العلاقة بين الساقين و وتر مثلث قائم الزاوية هي كالتالي:
c2=a2+b2
- c: وتر مثلث قائم الزاویة
- a: احد سيقان المثلث
- b: احدى سيقان المثلث الاخرى
إذا كان حجم أحد سيقان و وتر مثلث قائم الزاوية معروفًا، فيمكن الحصول على حجم الساق الأخرى من قانون فيثاغورس. نظرًا لأن الساقين والقاعدة والارتفاع متماثلين، يتم حساب مساحة المثلث باستخدام القانون العام.
A=a√c2 – a2 / 2
- A: المساحة
- a: احد سيقان مثلث قائم الزاویة
- c: وتر مثلث قائم الزاویة
مثال: حساب مساحة المثلث بالوتر
احسب مساحة مثلث قائم الزاوية بوتر بقيمة 5 وساق بقيمة 4. ما هو طول الساق الآخر في المثلث؟
عوض القيم المحددة في القانون:
A=a√52 – 42 / 2
A=2√25 – 16
A=2√9
A = 2×3 = 6
الأسئلة الشائعة حول مساحة المثلث
مساحة المثلث هي المنطقة المحصورة بين أضلاع المثلث الثلاثة.
قانون (الارتفاع × القاعدة) ÷ 2 هو القانون الأكثر أهمية المستخدم في الحسابات، ولكن هذا يعتمد أيضًا على ما إذا كنت تعرف الارتفاع والقاعدة أم لا.
عندما يتم إعطاء قيم أضلاع المثلث الثلاثة، يمكننا استخدام صيغة هرون لحساب مساحته، وفي هذه الطريقة، يجب أن نجد نصف محيط المثلث باستخدام الصيغة التي شرحناها أعلاه، ثم نستخدمها في صيغة هرون.
الخلاصة
من خلال قراءة هذه المقالة، تعرفتم على طرق حساب مساحة المثلث المتعددة، بدئاً من قانون الضرب في الارتفاع إلى استخدام قانون هرون وحتى أنواع المثلثات. يرافقك هذا الدليل خطوة بخطوة للحصول على فهم عميق لمفهوم المساحة وطرق حسابها المتنوعة.
المنابع المستخدمة
اختبار ذاتي لمساحة المثلث (quiz)
بناءً على كل ما قرأته، انقر فوق زر “البدء” واشترك في الاختبار بشكل اونلاين، ما عليك سوى حل 4 أسئلة حتى نتمكن من منحك الدرجة التي تستحقها.

8 تعليقات
ماعجبنيش الشرح ديرونا ديال السادس إبتدائي أكي
نعم
شكراً لرياضيات العربية على هذا المقال الجيد. لدي سؤال: إذا لم يكن ارتفاع المثلث محددًا في المسألة، فماذا أفعل؟
شكرًا على رأيك يا نينان العزيز، إذا كنت بحاجة إلى إيجاد مساحة المثلث بدون معرفة ارتفاع المثلث، أقترح عليك استخدام صيغة هرون التي استخدمناها في المقالة.
لم أفهم في الجزء الذي شرحتم فيه صيغة هرون من أين يجب أن أستخدم هذه الصيغة في حساباتي؟ وهل هذه الصيغة قابلة للتطبيق على جميع المثلثات؟
حسنًا يا ابوعيسی، إذا قرأت النص بعناية، فستفهم من أين يجب استخدام هذه الصيغة، لكنني سأشرح لك هنا حتى تتمكن من فهمها. تُستخدم صيغة هيرو او هرون لحساب مساحة مثلث بطول أضلاع b، c، و a، والتي تنطبق عندما نعرف قيم جميع أضلاع المثلث، واسم هذه الصيغة مأخوذة من اسم العالم الكبير هيرو السكندري او Hero of Alexandria
ماهي وحدة قياس مساحة المثلث؟
إنه سهل جدًا