مساحة المثلث القائم:القانون وتطبيقاتها العملية
مساحة المثلث قائم الزاوية تساوي القاعدة في الارتفاع على اثنين. وبالطبع من الممكن استخدام طرق أخرى مثل طريقة هيرون والجيب لحساب مساحة هذا النوع من المثلثات. ومع ذلك، عادةً ما تُستخدم نظرية فيثاغورس لتحديد الأحجام المختلفة لـ”مثلث قائم الزاويه”. في هذا المقال المقدم لكم على موقع الرياضيات العربية ، سوف نعلمك كيفية حساب مساحة المثلث قائم الزاوية مع حل عدة أمثلة مختلفة وعملية تماماً كما فعلنا في مقالة مساحة المثلث. بالإضافة إلى ذلك سوف نقوم بشرح حالات مثلث قائم الزاوية المختلفة لذا ابقوا معنا.
ما هو مثلث قائم الزاوية؟
المثلث القائم الزاوية هو مثلث بزاوية قائمة، أي أن إحدى زواياه تساوي 90 درجة. تقع هذه الزاوية بين ضلعين تسميان “الضلع الأفقي” و “الضلع العمودي”.
ما هي اجزاء مثلث قائم الزاوية؟
يتكون مثلث قائم الزاوية، مثل جميع المثلثات، من ثلاثة اضلاع (قاعدة)، وثلاثة ارتفاعات، وثلاثة رؤوس، وثلاث زوايا داخلية وثلاث زوايا خارجية.
في المثلث القائم الزاوية، تكون السیقان، ارتفاع مثلث قائم الزاوية والقاعدة متساوية مع بعضها البعض. بمعنى آخر، إذا كان حجم ساقي هذا المثلث معروفًا، يتم الحصول على مساحته باستخدام قانون القاعدة (أحد الساقين) في الارتفاع (الساق الآخرى) على اثنين.
طرق حساب مساحة المثلث القائم
يمكن حساب مساحة مثلث قائم الزاوية باستخدام جميع قوانين مساحة المثلث (القاعدة والارتفاع، هیرون والجيب). بالطبع، نظراً لوجود زاوية قائمة وإمكانية استخدام نظرية فيثاغورس، يمكن كتابة المزيد من القوانین لحساب مساحة مثلث قائم الزاوية.
أمثلة على حساب مساحة المثلث قائم
لدينا مثلث بضلعين معروفي القيمة 4 و 5. إذا كانت الزاوية بين هذين الضلعين 90 درجة، فكم ستكون مساحة المثلث؟
يتم الحصول على مساحة المثلث من القانون التالي:
2 ÷(ارتفاع × قاعدة) = مساحة المثلث
الصيغة الرياضية هي كما يلي:
A = b × h / 2
نعوض القيم المعروفة في القانون أعلاه:
A = 4×5 / 2
A = 20 / 2
A =10
اذاً مساحة المثلث يساوي 10
نظرية فيثاغورس لحساب مساحة المثلث قائم الزاوية
نظرية فيثاغورس هي مساواة بين تعبيرين جبريين توضح العلاقة بين طول الوتر وسيقان المثلث القائم الزاوية.
تُستخدم هذه النظرية في العديد من الحسابات الهندسية المتعلقة بالمثلثات القائمة.
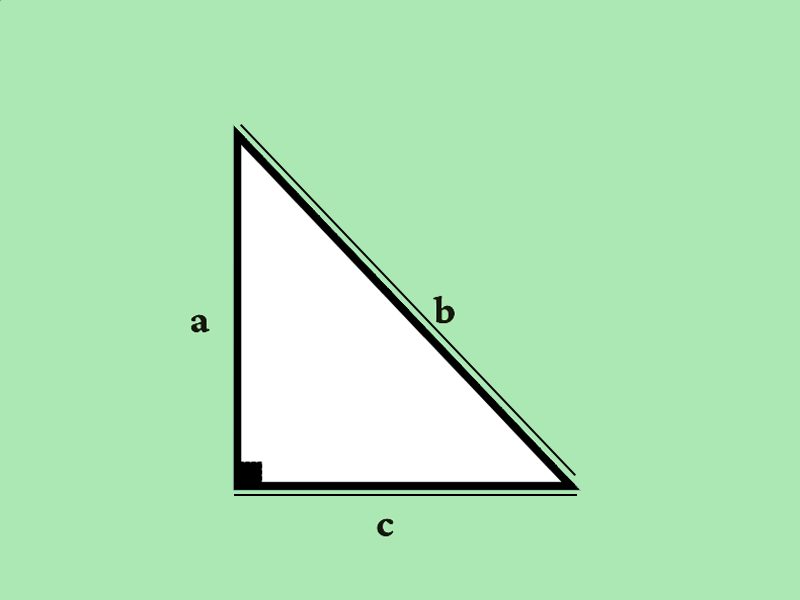
حسب العبارات في الصورة أعلاه فإن العلاقة بين الوتر وأرجل المثلث القائم تساوي:
c2=a2+b2
تسهل هذه النظرية حساب أبعاد المثلث القائم الزاوية والقوانين المخصصة له.
أمثلة على حساب مساحة المثلث قائم الزاوية بمعادلة فيثاغورس
اوجد مساحة مثلث قائم الزاوية مع وتر بقيمة 5 وضلع بقيمة 3.
بما أن لدينا حجم الوتر وأحد سيقان المثلث القائم الزاوية، فيمكن حساب حجم الساق الأخرى باستخدام معادلة فيثاغورس:
c2=a2+b2
- c:وتر يساوي 5
- a:احد السيقان يساوي 3
- b :ساق المثلث الاخر
52=32+b2
25=9+b2
16=b2
√16=b
4=b
بمعرفة قيمة الساق الأخرى، يمكننا استخدام قانون المساحة بناءً على القاعدة والارتفاع:
A = b × h / 2
A = 3×4 / 2
A = 12 / 2
A = 6
اذاً فإن مساحة المثلث تساوي 6
نظرة عامة على مساحة المثلث قائم
في هذه المقالة، قمنا بدراسة طرق حساب مساحة المثلث القائم الزاوية بعناية، تماماً كما فعلنا في مقالة محيط المثلث القائم. وقد شملت الطرق الشهيرة لحساب مساحة المثلث القائم الزاوية: ضرب نصف طول الضلعين القصيرين وتقسيم الناتج على 2 أو ضرب نصف محيط المثلث في طول الارتفاع.