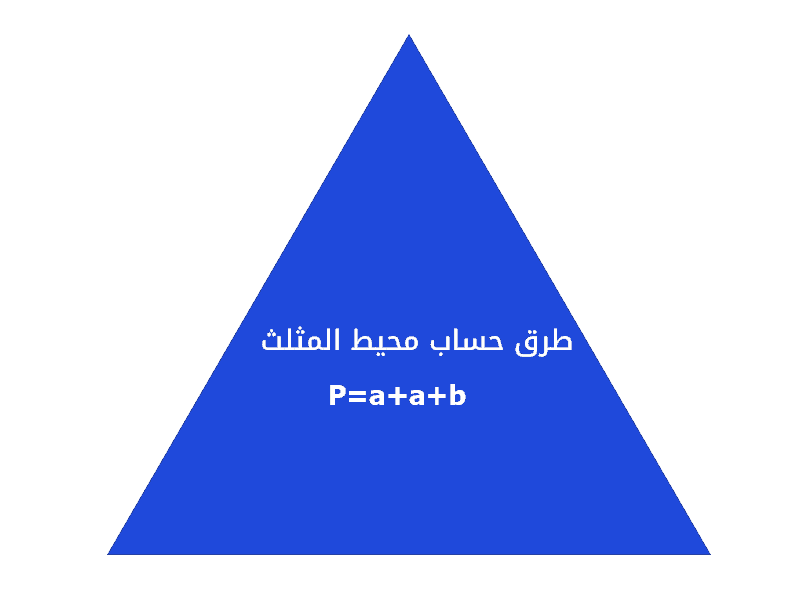
قانون محيط المثلث
يتم الحصول على محيط المثلث من مجموع أضلاعه الثلاثة. بالطبع، هذا في حال معرفة أحجام جميع اضلاع المثلث. بينما، في انواع المثلثات الاخرى مثل مثلث متساوي الساقين، ومثلث متساوي الأضلاع ومثلث قائم الزاوية، توجد علاقات خاصة لحساب المحيط.
ابقوا معنا في موقع الرياضيات العربية حتى نفحص معاً محيط المثلث بشكل كامل.
ما هو المثلث ؟
المثلث هو شكل له 3 اضلاع و 3 زوايا. يعتبر المثلث أحد الأشكال الهندسية الأساسية.
يمكن تقسيم العديد من الأشكال الهندسية والمضلعات إلى مجموعة من المثلثات.
ما هو محيط المثلث ؟
ان حجم اطراف أي شكل هو محيط ذلك الشكل. محيط المثلث هو حجم اطرافه أو مجموع أحجام الأضلاع المكونة له.
حساب محيط المثلث ببساطة
وفقًا لقانون محيط المثلث، فان محيط المثلث = الضلع الأول + الضلع الثاني + الضلع الثالث.
إذا كان لدينا مثلث بالأبعاد التالية:
- الضلع الأول : 4
- الضلع الثاني : 5
- الضلع الثالث : 6
محیط المثلث = 4+5+6 =15
اذاً محیط المثلث اعلاه يساوي 15.
ما استخدامات محيط المثلث؟
العديد من الأشياء والأماكن من حولنا على شكل مثلث. يستخدم المحيط لقياس الطول حول هذه العناصر. على سبيل المثال، إذا كان لدى شخص ما أرض مثلثة وأراد تحديد محيطها، فعليه استخدام قانون محيط المثلث.
محیط المثلث متساوي الساقین
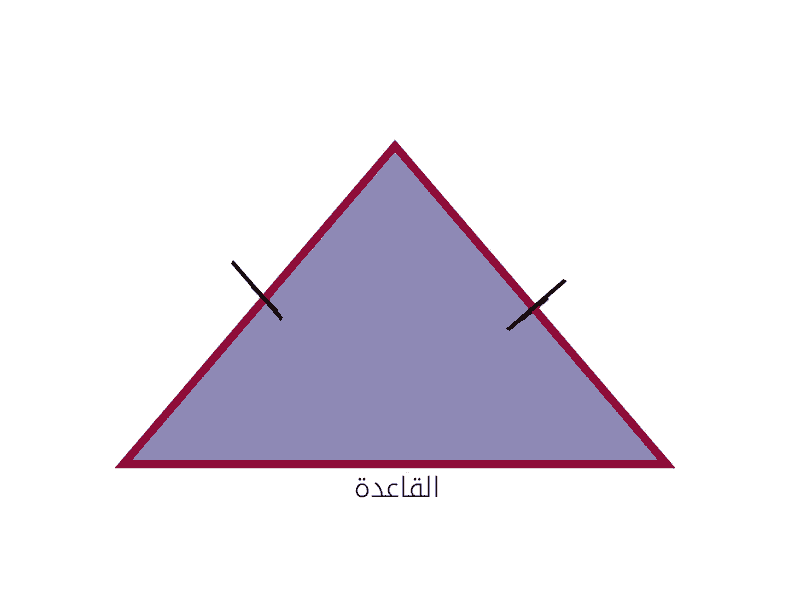
يعتبر المثلث الذي له ضلعين متساويين كمثلث متساوي الساقين. الأضلاع المتساوية لهذا المثلث تسمى “ساق” والجانب الثالث هو “القاعدة”. توضح الصورة أدناه مثالاً لمثلث متساوي الساقين. علامة | على أرجل هذا المثلث، تشير الى أن أحجامهما متساوية.
حساب محيط مثلث متساوي الضلعين
حساب محيط مثلث متساوي الضلعين في المثلث متساوي الساقين ادناه، جد طول الجزء المحدد بالرمز”؟” ثم أوجد محيط المثلث

المثلث أعلاه هو مثلث متساوي الساقين وحجم سيقانه يساوي 6. يتم حساب طول الجزء الغير معروف على النحو التالي:
الجزء المجهول + 2 = ساق المثلث
الجزء المجهول + 2 = 6
الجزء المجهول = 2 – 6
الجزء المجهول = 4
يتم الحصول على محيط المثلث بجمع أضلاعه الثلاثة
6 + 6 + 4 = محیط المثلث
16 = محیط المثلث
اذاً محیط المثلث يساوي 16.
محیط مثلث متساوی الساقین
في المثلث متساوي الساقين، يشار الى حجم الساق بـ a والقاعدة بـ b. نظرًا لأن أرجل هذا المثلث متساوية في الحجم، يتم استخدام الحرف a لتمثيل كلاهما.

بناءً على الصورة أعلاه، فإن الصيغة الرياضية أو التعبير الجبري لمحيط المثلث متساوي الساقين يساوي:
P=a+a+b
- P: محیط مثلث متساوی الساقین
- a: حجم ساق المثلث
- b: حجم قاعدة المثلث
نظرًا لأن الساقين (a) متساويين في الحجم، يمكننا جمعهما معًا وتمثيل الساقين بتعبير واحد:
P=2a+b
انواع المثلث
يمكن تصنيف المثلثات حسب طول اضلاعها أو حجم زواياها.
لتصنيف المثلثات بناءً على زواياها، يجب ان نقيس كل زاوية من زواياها الداخلية. يمكن تصنيف المثلثات على أساس الزوايا على النحو التالي:
- مثلث حاد
- مثلث قائم الزاویة
- مثلث منفرد
خصائص المثلث
- مجموع الزوايا الداخلية الثلاثة للمثلث يساوي دائمًا 180 درجة.
- دائمًا ما يكون مجموع طول ضلعي المثلث أكبر من طول الضلع الثالث.
- مساحة المثلث تساوي نصف حاصل ضرب قاعدته وارتفاعه